Cours de NSI Première
Constructions élémentaires Booléens Fonctions Chaînes de caractères Tableaux p-uplets et dictionnaires Tables de données Flottants Algorithmes classiques Index ÉnoncésDéfinition en extension, accès et modification de valeurs grâce à leur index, définition en compréhension, tris par sélection ou par insertion, tableaux à plusieurs dimensions
Un tableau permet de stocker en mémoire plusieurs valeurs dans une seule variable.
Une façon de définir un tableau est d'indiquer entre crochets les différentes valeurs, séparées par des virgules. On parle alors de définition en extension.
(1) Donner la définition en extension d'un tableau mois contenant les noms des six premiers mois de l'année (sous forme de chaînes de caractères).
mois = ['janvier', 'février', 'mars', 'avril', 'mai', 'juin']
(2) Après avoir exécuté les deux cellules suivantes, déterminer quel est le rôle de la fonction len.
jours = ['lundi', 'mardi', 'mercredi', 'jeudi', 'vendredi', 'samedi', 'dimanche']
len(jours)
len renvoie la longueur (c'est-à-dire le nombre d'éléments) du tableau qui est passé en paramètre.
Chaque valeur contenue dans un tableau est indexée par un entier supérieur ou égal à 0. Dans la mémoire de la machine, les valeurs sont stockées consécutivement. Pour accéder à la valeur de rang n d'un tableau tab, on utilise la notation tab[n].
(3) Modifier le code la cellule suivante pour faire apparaître la liste des jours de la semaine allant du 13 au 20 juillet 1789 : lundi 13 juillet 1789, mardi 14 juillet 1789, etc..
for k in range(len(jours)):
print(jours[k], 13 + k, 'juillet 1789')
Pour modifier la valeur de rang n contenue dans le tableau tab, il suffit d'utiliser une affectation du type tab[n] = nouvelle_valeur.
Mais si on tente d'accéder ou de modifier la nème valeur d'un tableau qui ne contient pas au moins n valeurs, alors une erreur se produit.
(4) Ecrire des lignes de code permettant à un utilisateur de remplacer le nom de chaque jour de la semaine par son équivalent en anglais.
for k in range(len(jours)):
jours[k] = input('Comment dit-on ' + jours[k] + ' en anglais ? ')
print(jours)
Si on souhaite stocker dans un tableau les carrés des nombres entiers compris entre 0 et 10, on peut définir le tableau en extension :
tab = [0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100]
On constate qu'une telle définition n'est pas pratique, voire impossible à mettre en oeuvre si le nombre de valeurs dans le tableau est grand.
On utilise alors une autre façon de définir le tableau : la définition en compréhension, qui est basée sur la notion de boucle.
tab = [k*k for k in range(11)] # le tableau est ici défini en compréhension
print(tab)
Elle permet d'obtenir rapidement des tableaux qui contiennent de nombreuses valeurs.
tab = [k*k for k in range(101)]
print(tab)
(5) Définir un tableau contenant le cube de tous les entiers compris entre 0 et 20.
print([k**3 for k in range(21)])
(6) Définir en une seule ligne de code un tableau composé de 100 entiers tirés au hasard entre 0 et 255.
from random import randint
tab_alea = [randint(0, 255) for _ in range(100)]
print(tab_alea)
Il est également possible d'ajouter une condition à la définition en compréhension.
Par exemple, pour obtenir le carré des nombres pairs compris entre 0 et 100, on écrit :
tab = [k*k for k in range(101) if k % 2 == 0]
print(tab)
(7) Définir un tableau contenant le cube de tous les entiers compris entre 0 et 20 et non multiples de 5.
tab = [k**3 for k in range(21) if k % 5 != 0]
print(tab)
k est multiple de 5 s'écrit en Python k % 5 == 0, et donc la condition k n'est pas multiple de 5 s'écrit k % 5 != 0.
Pour définir, par exemple, un tableau qui contient 100 fois la valeur 0, on peut écrire :
print([0 for _ in range(100)])
ou alors, de façon encore plus simple avec l'opérateur * :
print([0] * 100)
Enfin, l'opérateur + permet de concaténer (c'est-à-dire mettre bout à bout) plusieurs tableaux. Par exemple :
print([0]*5 + [1]*3 + [5*k for k in range(10) if k % 3 != 0])
(8) En une seule ligne de code, définir le tableau [0, 0, 0, 0, 4, 8, 12, 16, 20, ..., 92, 96, 100, 200, 400, 800, 1600, 3200, ..., 102400, 204800, 409600].
tab = [0]*3 + [4*k for k in range(25)] + [100*2**k for k in range(13)]
print(tab)
Remarquons enfin qu'en théorie la taille d'un tableau est fixée et ne peut pas être modifiée. En Python, les tableaux sont des tableaux dynamiques pour lesquels il est possible d'ajouter ou de retirer des éléments.
tab, on utilise l'instruction tab.append(element).n dans le tableau tab, on utilise l'instruction tab.insert(n, element).n dans le tableau tab, on utilise l'instruction del tab[n].Le but de cette partie est d'étudier deux algorithmes permettant de trier les élements d'un tableau du plus petit au plus grand. Les éléments peuvent être des nombres mais aussi, par exemple, des chaînes de caractères (ou tout autre objet dont le type possède un ordre total, c'est-à-dire un ordre pour lequel tout élément peut être comparé à tout autre élément).
(9) Ecrire la spécification de la fonction est_trie définie ci-dessous :
def est_trie(tab):
"""
Vérifie si un tableau est trié dans l'ordre croissant.
- Entrée : tab (tableau)
- Sortie : booléen (True si le tableau est trié, False sinon)
"""
for k in range(len(tab) - 1):
if tab[k] > tab[k + 1]:
return False
return True
Les tableaux suivants sont triés :
tableau_entiers = [-2, 0, 5, 9, 12]
est_trie(tableau_entiers)
tableau_flottants = [-1.3, -1.0, 0.001, 0.1, 0.15]
est_trie(tableau_flottants)
tableau_chaines = ['arbre', 'bonbon', 'bonjour', 'bouteille', 'bu']
est_trie(tableau_chaines)
Le principe du tri par sélection est le suivant :
De cette façon, la partie de gauche du tableau est triée en permanence, et les éléments y sont placés à leur position définitive.

Algorithme de tri par sélection
Début
n ← longueur du tableau tab
Pour k allant de 0 à (n-2) faire
i ← index du plus petit élement de tab dont l'index est compris entre k et (n-1)
Echanger le kème élement et le ième élement du tableau tab
Fin Pour
Fin
(10) Ecrire une fonction index_min prenant en paramètres d'entrée un tableau tab et un entier k et renvoyant l'index du plus petit élement du tableau tab parmi les éléments dont l'index est supérieur ou égal à k.
def index_min(tab, k):
"""
Recherche quel est l'index du plus petit élément du tableau tab ayant un index supérieur ou égal à k.
- Entrées : tab (tableau), k (entier)
- Sortie : m (entier)
"""
i_min = k
for i in range(k + 1, len(tab)):
if tab[i] < tab[i_min]:
i_min = i
return i_min
On peut alors définir la fonction tri_selection :
def tri_selection(tab):
"""
Trie un tableau grâce à l'algorithme de tri par sélection.
- Entrée : tab (tableau)
- Effet de bord : modification du tableau passé en paramètre d'entrée
"""
for k in range(len(tab) - 1):
i = index_min(tab, k)
tab[k], tab[i] = tab[i], tab[k]
from random import randint
tab = [randint(0, 100) for _ in range(20)]
print('Tableau non trié : ', tab)
tri_selection(tab)
print('Tableau trié : ', tab)
Le principe du tri par insertion est le suivant :
De cette façon, la partie de gauche du tableau est triée en permanence mais les éléments n'y sont pas placés à leur position définitive.

Algorithme de tri par insertion
Début
n ← longueur du tableau tab
Pour k allant de 1 à (n-1) faire
valeur ← tab[k]
pos ← k
Tant que pos > 0 et tab[pos - 1] > valeur faire
tab[pos] ← tab[pos - 1]
pos ← pos - 1
Fin Tant que
tab[pos] ← valeur
Fin Pour
Fin
(11) Ecrire une fonction tri_insertion prenant en paramètre d'entrée un tableau tab et triant les éléments du tableau grâce à l'algorithme de tri par insertion.
def tri_insertion(tab):
"""
Trie un tableau grâce à l'algorithme de tri par insertion.
- Entrée : tab (tableau)
- Effet de bord : modification du tableau passé en paramètre d'entrée
"""
for k in range(1, len(tab)):
valeur = tab[k]
pos = k
while pos > 0 and tab[pos-1] > valeur:
tab[pos] = tab[pos-1]
pos = pos - 1
tab[pos] = valeur
tab = [randint(0, 100) for _ in range(20)]
print('Tableau non trié : ', tab)
tri_insertion(tab)
print('Tableau trié : ', tab)
Pour tester l'efficacité des algorithmes de tri par sélection et par insertion, on peut commencer par mesurer le temps qui leur est nécessaire pour trier des tableaux contenant de nombreux éléments. La fonction time du module time permet d'effectuer cette mesure.
from time import time
Voici comment mesurer le temps que met l'ordinateur pour compter de 1 à 1000000 :
tps_debut = time()
i = 1
while i < 1000000:
i = i + 1
tps_fin = time()
print('Temps d\'exécution :', tps_fin - tps_debut, 's')
(12) Comparer le temps mis par chacun des deux algorithmes pour trier un tableau contenant 1000 valeurs, puis 2000 valeurs, puis 4000 valeurs :
tab = [randint(0, 1000) for k in range(1000)] # 1000 éléments aléatoires dans un tableau
# tab = [1000 - k for k in range(1000)] # 1000 éléments dans l'ordre décroissant
# tab = [k for k in range(1000)] # 1000 éléments dans l'ordre croissant
tps_debut = time()
tri_selection(tab)
tps_fin = time()
duree_calcul = tps_fin - tps_debut
print('Durée du tri par sélection pour 1000 éléments : ', duree_calcul, 's')
tab = [randint(0, 1000) for k in range(1000)] # 1000 éléments aléatoires dans un tableau
# tab = [1000 - k for k in range(1000)] # 1000 éléments dans l'ordre décroissant
# tab = [k for k in range(1000)] # 1000 éléments dans l'ordre croissant
tps_debut = time()
tri_insertion(tab)
tps_fin = time()
duree_calcul = tps_fin - tps_debut
print('Durée du tri par insertion pour 1000 éléments : ', duree_calcul, 's')
Nous avons vu jusqu'à présent des tableaux contenant des valeurs de type entier ou de type chaîne de caractères, mais les valeurs peuvent en réalité être de n'importe quel type.
En particulier, un tableau peut contenir des tableaux. On parle alors de tableau à deux dimensions.
Par exemple, le tableau union_europeenne défini ci-dessous est un tableau à deux dimensions contenant 27 tableaux qui correspondent à chaque état-membre de l'UE. On stocke en mémoire l'équivalent d'un tableau composé de 27 lignes et 2 colonnes.
union_europeenne = [
['Allemagne', 'Berlin'], ['Belgique', 'Bruxelles'], ['France', 'Paris'],
['Luxembourg', 'Luxembourg'], ['Italie', 'Rome'], ['Pays-Bas', 'Amsterdam'],
['Danemark', 'Copenhague'], ['Irlande', 'Dublin'], ['Grèce', 'Athènes'],
['Espagne', 'Madrid'], ['Portugal', 'Lisbonne'], ['Autriche', 'Vienne'],
['Finlande', 'Helsinki'], ['Suède', 'Stockholm'], ['Chypre', 'Nicosie'],
['Estonie', 'Tallinn'], ['Hongrie', 'Budapest'], ['Lettonie', 'Riga'],
['Lituanie', 'Vilnius'], ['Malte', 'La Valette'], ['Pologne', 'Varsovie'],
['République Tchèque', 'Prague'], ['Slovaquie', 'Bratislava'], ['Slovénie', 'Ljubljana'],
['Bulgarie', 'Sofia'], ['Roumanie', 'Bucarest'], ['Croatie', 'Zagreb']
]
L'élément du tableau union_européenne indexé par l'entier 2 est un tableau contenant des chaînes de caractères.
Il correspond à la troisième ligne de union_europeenne.
union_europeenne[2]
Dans un tableau à deux dimensions, on utilise une double indexation pour accéder aux éléments du tableau . Le premier indice correspond au numéro de ligne (ici rang du pays dans le tableau union_europeenne) et le second au numéro de colonne (ici 0 pour le nom du pays et 1 pour sa capitale):
print(union_europeenne[2][1], 'est la capitale de', union_europeenne[2][0])
(13) Afficher les capitales des pays de l'Union Européenne, séparées par des espaces.
for k in range(28):
print(union_europeenne[k][1], end = ' ')
(14) Afficher la liste des pays de l'Union Européenne, séparés par des espaces.
for k in range(len(union_europeenne)):
print(union_europeenne[k][0], end = ' ')
for pays in union_europeenne:
print(pays[0], end = ' ')
pays remplace
union_europeenne[k].len pour déterminer le nombre d'éléments d'un tableau.tableau sont compris entre 0 et len(tableau)-1.* et + sur des tableaux.tab.append(elem), tab.insert(n, elem) et del tab[n].time du module time.(1) Ecrire une fonction tab_alea qui prend en paramètre d'entrée un entier positif n et qui renvoie un tableau composé de n entiers tirés au hasard et compris entre 0 et 255.
from random import randint
def tab_alea(n):
"""
Retourne un tableau composé de n entiers compris entre 0 et 255.
- Entrée : n (entier positif)
- Sortie : tab (tableau)
Attention : importer la fonction randint du module random
"""
if type(n) != int:
raise TypeError('l\'argument doit être entier')
if n < 0:
raise ValueError('l\'argument doit être positif')
return [randint(0, 255) for k in range(n)]
mon_tableau = tab_alea(10)
print(mon_tableau)
(2) Ecrire une fonction somme_des_valeurs qui prend en paramètre d'entrée un tableau de valeurs entières et qui renvoie la somme de toutes les valeurs contenues dans le tableau.
def somme_des_valeurs(tab):
"""
Calcule la somme des valeurs contenues dans un tableau.
- Entrée : tab (tableau composé d'entiers)
- Sortie : somme (entier)
"""
if type(tab) != list:
raise TypeError('l\'argument doit être un tableau')
somme = 0
for valeur in tab:
if type(valeur) != int:
raise ValueError('l\'argument doit être un tableau contenant des entiers')
somme = somme + valeur
return somme
total = somme_des_valeurs(mon_tableau)
print(total)
(3) Utiliser la fonction somme_des_valeurs pour définir une fonction valeur_moyenne qui prend en paramètre d'entrée un tableau de valeurs entières et qui renvoie la moyenne des valeurs contenues dans le tableau.
def valeur_moyenne(tab):
"""
Calcule la valeur moyenne contenue dans un tableau.
- Entrée : tab (tableau composé d'entiers)
- Sortie : (flottant)
"""
somme = somme_des_valeurs(tab)
if len(tab) == 0:
raise ValueError('l\'argument doit être un tableau non vide')
else:
return somme / len(tab)
moyenne = valeur_moyenne(mon_tableau)
print(moyenne)
(4) Ecrire une fonction valeur_maximale qui prend en paramètre d'entrée un tableau de valeurs entières et qui renvoie la plus grande des valeurs contenues dans le tableau.
def valeur_maximale(tab):
"""
Détermine la plus grande des valeurs contenues dans un tableau.
- Entrée : tab (tableau composé d'entiers)
- Sortie : maximum (entier)
"""
if type(tab) != list:
raise TypeError('l\'argument doit être un tableau')
if len(tab) == 0:
raise ValueError('l\'argument doit être un tableau non vide')
maximum = tab[0]
for valeur in tab:
if type(valeur) != int:
raise ValueError('l\'argument doit être un tableau contenant des entiers')
if valeur > maximum:
maximum = valeur
return maximum
maxi = valeur_maximale(mon_tableau)
print(maxi)
(5) Pour mélanger les valeurs contenues dans un tableau, on peut utiliser l'algorithme de Knuth (également appelé algorithme de Fisher-Yates) :
Algorithme de Knuth ou de Fisher-Yates pour le mélange des éléments d'un tableau
Début
n ← longueur du tableau tab
Pour i allant de 0 à (n-2) faire
j ← entier aléatoire compris entre i et (n-1)
Echanger le ième élement et le jème élement du tableau tab
Fin Pour
Retourner tab
Fin
Ecrire une fonction melange prenant en paramètre d'entrée un tableau et renvoyant un tableau mélangé grâce à l'algorithme de Knuth.
from random import randint
def melange(tab):
"""
Mélange les valeurs contenues dans le tableau via l'algorithme de Knuth.
- Entrée : tab (tableau de nombres)
- Sortie : tab (tableau)
Attention : importer la fonction randint du module random.
"""
n = len(tab)
for i in range(n-1):
j = randint(i, n-1)
tab[i], tab[j] = tab[j], tab[i]
return tab
mon_tableau = melange(mon_tableau)
print(mon_tableau)
Le but de cet exercice est d'afficher à l'écran des cases grises dans une fenêtre graphique Pygame.
Exécuter la cellule suivante :
from cases_grises import *
Deux fonctions ouverture_fenetre et affichage_cases sont maintenant disponibles en mémoire. On en donne un exemple d'utilisation dans la cellule suivante.
La variable tab contient un tableau composé de 20 entiers compris entre 0 et 255. A chaque entier correspond une nuance de gris, foncée pour un entier proche de 0 et claire pour un entier proche de 255. En appelant successivement la fonction ouverture_fenetre et la procédure affichage_cases, on obtient un affichage à l'écran de cases dont la nuance de gris correspond aux valeurs stockées dans le tableau.

tab = [0, 0, 15, 30, 45, 60, 75, 90, 105, 120, 135, 150, 165, 180, 195, 210, 225, 240, 255, 255]
fenetre = ouverture_fenetre() # la fonction ouverture_fenetre renvoie une variable fenetre
affichage_cases(fenetre, tab) # la procédure affichage_cases dessine des carrés gris dans la fenêtre
(1) Modifier la définition du tableau tab dans le but d'obtenir les affichages ci-dessous :

# Affichage 1
tab = [128] * 20
fenetre = ouverture_fenetre()
affichage_cases(fenetre, tab)

# Affichage 2
tab = [255]*10 + [0]*10
fenetre = ouverture_fenetre()
affichage_cases(fenetre, tab)

# Affichage 3
from random import randint
tab = [randint(0, 255) for _ in range(20)]
fenetre = ouverture_fenetre()
affichage_cases(fenetre, tab)

# Affichage 4
tab = [255] + [255 - 15*k for k in range(18)] + [0]
fenetre = ouverture_fenetre()
affichage_cases(fenetre, tab)
En réalisant plusieurs affichages successifs, on obtient une animation plutôt qu'une image statique. On peut utiliser la procédure sleep du module time pour faire en sorte qu'une pause de quelques millisecondes ait lieu entre les différents affichages.
from time import sleep
fen = ouverture_fenetre()
for i in range(0, 256, 16):
tab = [i]*10 + [255-i]*10
affichage_cases(fen, tab)
sleep(0.2) # Pause de 200 ms (soit 0.2 s) entre chaque affichage
(2) Faire en sorte d'obtenir l'affichage ci-dessous :
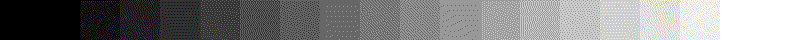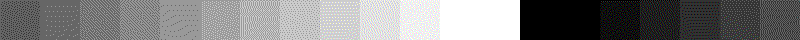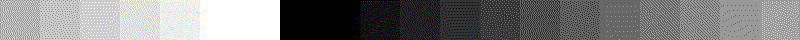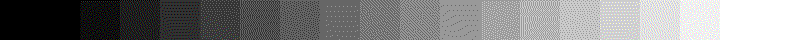
fen = ouverture_fenetre()
tab = [0] + [15*k for k in range(18)] + [255]
for _ in range(100):
tab.append(tab[0]) # ajoute le premier élément du tableau à la fin du tableau
del tab[0] # supprime le premier élément du tableau
affichage_cases(fen, tab)
sleep(0.2)
Pour fermer la fenêtre Pygame, il suffit d'exécuter la commande suivante :
pygame.quit()
(1) Définir en compréhension un tableau à deux dimensions table_addition contenant sur 11 lignes et 11 colonnes les valeurs de i + j, pour i et j compris entre 0 et 10.
table_addition = [[i + j for j in range(11)] for i in range(11)]
print(table_addition)
Après avoir exécuté la cellule suivante, vous pouvez utiliser la fonction affichage_table qui prend en entrée un tableau à deux dimensions et qui l'affiche dans une fenêtre Pygame.
from tables import affichage_table
affichage_table(table_addition)

(2) Modifier la définition de table_addition pour faire en sorte d'ajouter une ligne et une colonne d'en-tête. Le but est d'obtenir :
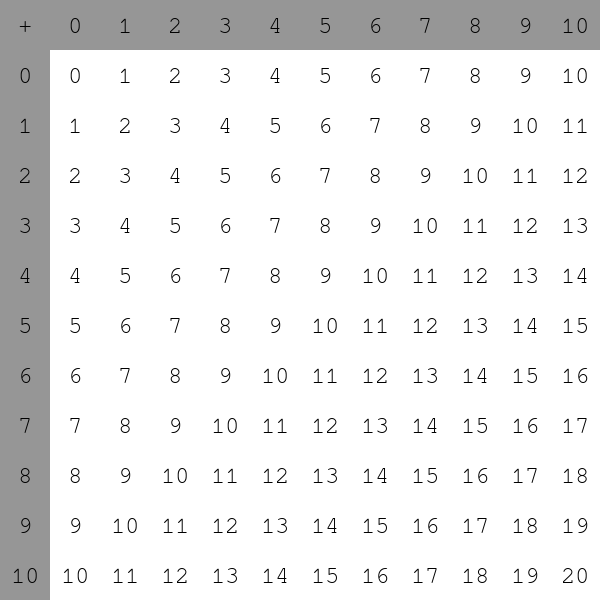 |
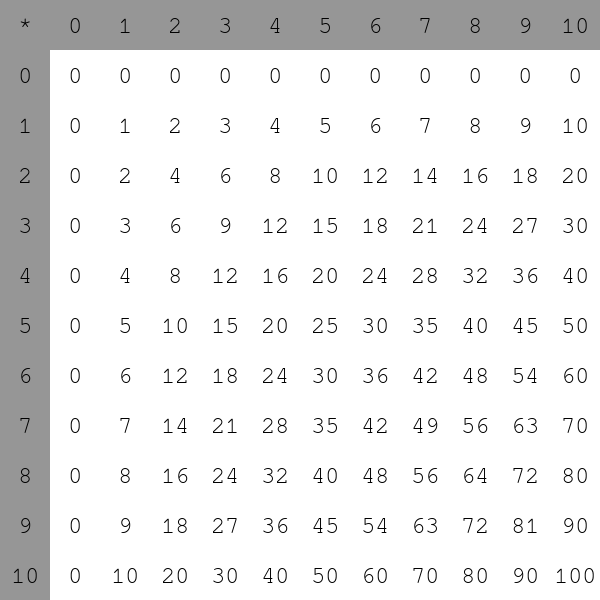 |
table_addition = [['+'] + [k for k in range(11)]] + [[i] + [i + j for j in range(11)] for i in range(11)]
affichage_table(table_addition)
table_multiplication = [['*'] + [k for k in range(11)]] + [[i] + [i * j for j in range(11)] for i in range(11)]
affichage_table(table_multiplication)