Chapitre 9 : Algorithmes classiques¶

Recherche dichotomique dans un tableau trié, algorithmes gloutons, algorithme des k plus proches voisins

Partie A - Recherche d'une valeur dans un tableau¶

L'objectif de cette partie est d'écrire un algorithme qui détermine si une valeur v est présente ou non dans un tableau tab.

Recherche séquentielle¶

La première idée que nous pouvons avoir pour rechercher une valeur dans un tableau, c'est de parcourir le tableau et de regarder si les éléments successifs du tableau correspondent à la valeur cherchée. On parle de recherche séquentielle.

Voici deux illustrations pour des tableaux de 40 éléments dans lesquels on recherche la valeur 63.

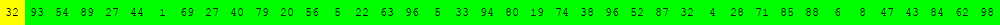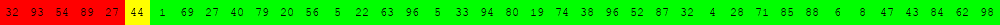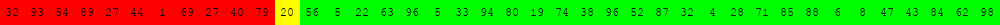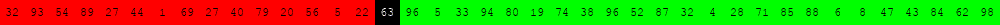
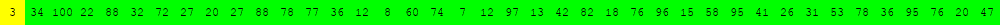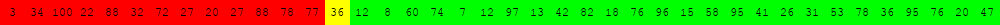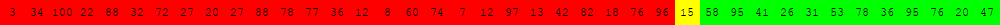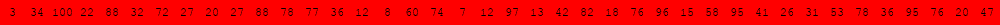
En vert, la partie du tableau où la valeur cherchée est susceptible de se trouver. En jaune, la valeur regardée.

Algorithme de recherche séquentielle d'une valeur v dans un tableau tab

Début

Pour k allant de 0 à longueur(tab)-1 faire

Si tab[k] = v alors

Retourner Vrai

Fin Si

Fin Pour

Retourner Faux

Fin

Question 1 : Ecrire le code de la fonction recherche qui parcourt le tableau tab et qui retourne True si la valeur v est trouvée dans le tableau et False sinon.

def recherche(tab, v):
    """
    Recherche la présence ou l'absence d'une valeur v dans un tableau tab
    - Entrées : tab (tableau), v
    - Sortie : (booléen égal à True si la valeur v est présente dans le tableau tab, et False sinon)
    """
    for k in range(len(tab)):
        if tab[k] == v:
            return True
    return False

print(recherche([0, 3, 1, 7, 4, 9, 5, 1, 6, 8], 5))

True

print(recherche([0, 3, 1, 7, 4, 9, 5, 1, 6, 8], 2))

False

Question 2 : Mesurer le temps d'exécution de la fonction recherche dans le cas où v = 63 et où :

tab contient 1000 éléments choisis au hasard entre 0 et 2000,
tab contient 100000 éléments choisis au hasard entre 0 et 200000,
tab contient 10000000 éléments choisis au hasard entre 0 et 20000000.

Pour chaque situation, faire 10 mesures et calculer la moyenne des 10 temps d'exécution obtenus.

from random import randint
from time import perf_counter

def mesure_duree_recherche(nb_mesures, taille_tableau):
    """
    Calcule la durée moyenne d'exécution de la fonction recherche
    - Entrées : nb_mesures (entier), taille_tableau (entier)
    - Sortie : duree (flottant)
    """
    duree = 0
    for _ in range(nb_mesures):
        # Création d'un tableau
        tableau = [randint(0, 2*taille_tableau) for _ in range(taille_tableau)]
        # Mesure de la durée d'exécution de recherche(tableau, 63)
        tps_debut = perf_counter()
        recherche(tableau, 63)
        tps_fin = perf_counter()
        duree = duree + tps_fin - tps_debut
    return duree / nb_mesures

n = 1000
print('Durée moyenne de la recherche pour', n, 'élements :', mesure_duree_recherche(10, n), 's')

Durée moyenne de la recherche pour 1000 élements : 0.0001421868002580595 s

n = 100000
print('Durée moyenne de la recherche pour', n, 'élements :', mesure_duree_recherche(10, n), 's')

Durée moyenne de la recherche pour 100000 élements : 0.011037535699870205 s

n = 10000000
print('Durée moyenne de la recherche pour', n, 'élements :', mesure_duree_recherche(10, n), 's')

Durée moyenne de la recherche pour 10000000 élements : 1.1446741988998839 s

Voici les durées moyennes d'exécution de la fonction recherche mesurées pour des tableaux de différentes tailles :

Taille du tableau (nombre d'éléments)	1 000	10 000	100 000	1 000 000	10 000 000
Durée moy. de recherche (millisecondes)	0,1	1,2	11,0	116,2	1144,7

Dans le pire des cas (cas où le tableau tab ne contient pas la valeur v), la fonction recherche parcourt le tableau en entier. Le temps d'exécution est alors proportionnel à la taille du tableau. On dit que la recherche séquentielle a une complexité linéaire.

Question 3 : Déterminer l'ordre de grandeur du temps d'exécution (dans le pire cas) de la fonction recherche pour un tableau qui contiendrait un milliard de valeurs, et pour un tableau qui contiendrait mille milliards de valeurs.

Voici l'ordre de grandeur de la durée d'exécution de la fonction recherche pour des tableaux de très grande taille :

Taille du tableau (nombre d'éléments)	10 000 000	1 000 000 000	1 000 000 000 000
Durée d'exécution estimée (secondes)	1	100	100 000
Durée d'exécution estimée (ordre de grandeur)	seconde	minute	jour

Recherche dichotomique dans un tableau trié¶

Dans le cas d'un tableau trié, il existe un algorithme beaucoup plus efficace pour déterminer si une valeur est présente ou non dans le tableau : l'algorithme de recherche dichotomique. Il s'agit d'un algorithme dont le principe est diviser pour régner.

On regarde d'abord la valeur située au milieu du tableau.

Si la valeur médiane est supérieure à la valeur cherchée, cela signifie que la valeur cherchée ne peut être que dans la première moitié du tableau. On recommence donc l'opération sur la première moitié du tableau.
Si la valeur médiane est inférieure à la valeur cherchée, cela signifie que la valeur cherchée ne peut être que dans la seconde moitié du tableau. On recommence donc l'opération sur la seconde moitié du tableau.

Voici deux illustrations pour des tableaux triés de 40 éléments dans lesquels on recherche la valeur 63.

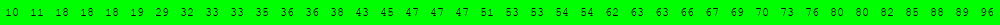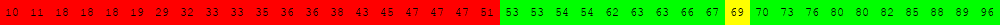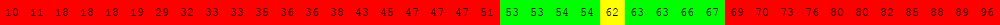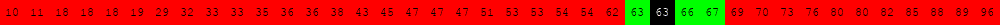
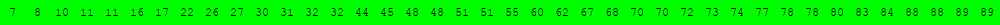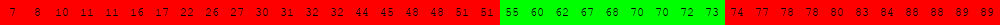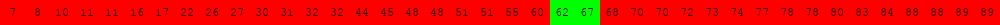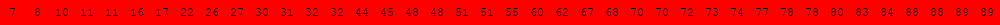
En vert, la partie du tableau où la valeur cherchée est susceptible de se trouver. En jaune, la valeur médiane à chaque étape.

L'exécution des deux cellules suivantes permet d'obtenir d'autres illustrations du même type.

from dichotomie import illustration_dichotomie
from random import randint

tableau = sorted([randint(0, 100) for _ in range(40)])
illustration_dichotomie(tableau, 63)

On donne l'algorithme de recherche dichotomique en français :

Algorithme de recherche dichotomique d'une valeur v dans un tableau trié tab

Début

g ← 0

d ← (longueur du tableau tab) - 1

Tant que g ≤ d faire

m ← valeur moyenne de g et d (arrondi entier par défaut)

Si tab[m] > v alors

d ← m - 1

Sinon si tab[m] < v alors

g ← m + 1

Sinon

Retourner Vrai

Fin Si

Fin Tant que

Retourner Faux

Fin

Question 4 : Implémenter l'algorithme ci-dessus sous la forme d'une fonction dichotomie prenant deux paramètres d'entrée.

def dichotomie(tab, v):
    """
    Recherche par dichotomie la présence ou l'absence d'une valeur v dans un tableau tab
    - Entrées : tab (tableau), v
    - Sortie : (booléen égal à True si la valeur v est présente dans le tableau tab, et False sinon)
    """
    g = 0
    d = len(tab) - 1
    while g <= d:
        m = (g + d) // 2
        if tab[m] > v:
            d = m - 1
        elif tab[m] < v:
            g = m + 1
        else:
            return True
    return False

print(dichotomie([0, 1, 1, 3, 4, 5, 6, 7, 8, 9], 5))

True

print(dichotomie([0, 1, 1, 3, 4, 5, 6, 7, 8, 9], 2))

False

Correction de l'algorithme de recherche dichotomique¶

Pour savoir si un algorithme fait ce qu'on attend de lui, il faut se poser deux questions :

Est-ce que l'algorithme se termine et renvoie un résultat ? Une preuve de terminaison permet de répondre oui.
Est-ce qu'un résultat renvoyé par l'algorithme est correct ? Une preuve de correction partielle permet de répondre oui.

Répondre oui aux deux questions à la fois, c'est prouver la correction totale de l'algorithme, c'est-à-dire prouver que l'algorithme remplit son rôle.

Terminaison de l'algorithme de recherche dichotomique pour prouver que l'algorithme renvoie toujours un résultat¶

Il y a deux cas possibles : soit tab[m] est égal à la valeur cherchée v lors d'un des tours de boucle, soit tab[m] n'est jamais égal à v.

Dans le premier cas, les deux conditions tab[m] > v et tab[m] < v sont fausses toutes les deux, et donc l'instruction Retourner Vrai est exécutée. Cela prouve que l'algorithme termine dans ce premier cas.

Dans le second cas, l'instruction Retourner Vrai n'est jamais exécutée. Il faut donc s'assurer que la boucle Tant s'interrompt nécessairement au bout d'un certain nombre d'itérations, permettant l'exécution de l'instruction Retourner Faux.

Pour justifier qu'il ne peut y avoir de boucle infinie, on considère le nombre d - g + 1, qui correspond au nombre d'éléments du tableau dont l'indice est compris entre g et d. Il s'agit du nombre d'éléments affichés en vert sur les illustrations précédentes. Ce nombre d - g + 1 est appelé un variant de boucle, parce que sa valeur change à chaque itération. Plus précisément, il s'agit d'une valeur entière qui diminue au moins d'une unité à chaque itération (en fait, elle est au moins divisée par 2 pour l'algorithme de recherche dichotomique), et qui finit donc par devenir nulle.

On en déduit que, au bout d'un certain nombre d'itérations, d - g + 1 = 0, d'où d = g - 1. La condition g ≤ d finit donc par être fausse, ce qui interrompt la boucle Tant que.

Correction partielle de l'algorithme de recherche dichotomique pour prouver que le résultat renvoyé est toujours le bon¶

Il y a deux cas possibles : soit l'algorithme renvoie Vrai, soit il renvoie Faux.

Dans le premier cas, l'algorithme a renvoyé Vrai parce que les deux conditions tab[m] > v et tab[m] < v étaient fausses. Autrement dit, tab[m] était égal à la valeur cherchée v, et l'algorithme a donc eu raison de renvoyer Vrai.

Dans le second cas, l'algorithme a renvoyé Faux parce que la boucle Tant que a terminé son exécution. Il faut justifier que, dans ce cas, la valeur v ne pouvait pas être présente dans le tableau.

On considère pour cela la propriété << la valeur v ne peut qu'avoir un indice compris entre g et d >>. Autrement dit, la valeur v ne peut être que parmi les éléments affichés en vert sur les illustrations précédentes. Cette propriété est appelée un invariant de boucle, parce qu'elle est reste vraie à chaque itération.

Avant la première itération, g et d sont les indices des extrémités du tableau, et donc la propriété est évidemment vraie. Elle reste vraie après chaque itération parce que le tableau est trié et parce que :

dans le cas où tab[m] > v, la valeur v ne peut qu'avoir un indice compris entre g et m-1 (valeur qu'on affecte à d).
dans le cas où tab[m] < v, la valeur v ne peut qu'avoir un indice compris entre m+1 (valeur qu'on affecte à g) et d.

Complexité de l'algorithme de recherche dichotomique¶

Question 5 : Quel est, dans le pire cas, le nombre d'itérations de la boucle Tant que, lorsque tab contient :

1 000 éléments ?
1 000 000 éléments ?
1 000 000 000 éléments ?
1 000 000 000 000 élements ?

Lors d'une recherche dichotomique, la taille de la partie (verte) du tableau où se trouve potentiellement la valeur cherchée est (au moins) divisée par 2 à chaque itération de la boucle Tant que. Si n désigne la taille du tableau, alors le nombre d'itérations de la boucle Tant que, dans le pire des cas, est le plus petit entier k tel que $2^k > n$.

Taille du tableau (nombre d'éléments)	1 000	1 000 000	1 000 000 000	1 000 000 000 000
Nombre d'itérations de la boucle Tant que (dans le pire des cas)	10	20	30	40

Le temps d'exécution de la fonction dichotomie est proportionnel au nombre d'itérations de la boucle Tant que. L'algorithme de recherche dichotomique est donc extrêmement efficace, puisqu'une multiplication par 1000 de la taille du tableau entraîne simplement 10 itérations supplémentaires. On dit que la recherche dichotomique a une complexité logarithmique. Rappelons cependant qu'elle n'est possible que si le tableau est trié.

Partie B - Algorithmes gloutons¶

L'objectif de cette partie est de découvrir un type d'algorithmes particuliers, les algorithmes gloutons, qui sont utilisés pour résoudre des problèmes d'optimisation : on recherche, parmi de nombreuses solutions possibles d'un problème, une solution qui soit meilleure que les autres, selon un critère donné.

Problème du rendu de monnaie¶

Un commerçant souhaite rendre la monnaie à son client en utilisant le moins de pièces possibles. On suppose que le commerçant dispose d'une quantité importante de chaque pièce et que les pièces disponibles sont les suivantes :

Question 6 : Quel est le plus petit nombre de pièces possible dans le cas où le commerçant doit rendre 16 centimes ? 1 euro et 62 centimes ? Expliquer la méthode utilisée.

XXX

On donne maintenant l'algorithme suivant, appelé algorithme glouton pour le rendu du monnaie.

Algorithme glouton pour le rendu de monnaie lorsque la somme à rendre est de S centimes

Début

pieces ← [200, 100, 50, 20, 10, 5, 2, 1]

k ← 0

nb_pieces_rendues ← 0

Tant que S > 0 faire

Si S ≥ pieces[k] alors

S ← S - pieces[k]

nb_pieces_rendues ← nb_pieces_rendues + 1

Sinon

k ← k + 1

Fin Si

Fin Tant que

Retourner nb_pieces_rendues

Fin

Question 7 : Ecrire le code de la fonction rendre_monnaie qui prend en paramètre d'entrée un entier S correspondant à la somme à rendre (en centimes) et qui retourne le nombre minimal de pièces à rendre.

def rendre_monnaie(S):
    """
    Détermine (par méthode gloutonne) le nombre minimal de pièces à rendre pour rendre S centimes
    - Entrées : S (entier)
    - Sortie : nb_pieces_rendues (entier)
    """
    pieces = [200, 100, 50, 20, 10, 5, 2, 1]
    k = 0
    nb_pieces_rendues = 0
    while S > 0:
        if S >= pieces[k]:
            S = S - pieces[k]
            nb_pieces_rendues = nb_pieces_rendues + 1
        else:
            k = k + 1
    return nb_pieces_rendues

rendre_monnaie(16)

3

rendre_monnaie(162)

4

Question 8 : Réécrire le code de la fonction rendre_monnaie pour qu'elle retourne le nombre de pièces à rendre de chaque type.

def rendre_monnaie(S):
    """
    Détermine (par méthode gloutonne) les pièces à rendre pour rendre S centimes
    - Entrées : S (entier)
    - Sortie : pieces_rendues (dictionnaire ayant pour clés les différents types de pièeces)
    """
    pieces = [200, 100, 50, 20, 10, 5, 2, 1]
    k = 0
    pieces_rendues = {valeur : 0 for valeur in pieces}
    while S > 0:
        if S >= pieces[k]:
            S = S - pieces[k]
            pieces_rendues[pieces[k]] = pieces_rendues[pieces[k]] + 1
        else:
            k = k + 1
    return pieces_rendues

rendre_monnaie(16)

{200: 0, 100: 0, 50: 0, 20: 0, 10: 1, 5: 1, 2: 0, 1: 1}

rendre_monnaie(162)

{200: 0, 100: 1, 50: 1, 20: 0, 10: 1, 5: 0, 2: 1, 1: 0}

XXX

On peut démontrer que l'algorithme glouton pour le rendu de monnaie donne toujours une réponse optimale lorsqu'on utilise les pièces en euros. Mais ce n'est pas le cas dans n'importe quel système monétaire.

Question 9 : Imaginons un système monétaire où les seules pièces disponibles seraient des pièces de 10 centimes, de 6 centimes et de 1 centime. Quel rendu de monnaie l'algorithme glouton proposerait-il pour une somme à rendre de 12 centimes ? Cette solution serait-elle optimale ?

XXX

Partie C - Algorithme des k plus proches voisins¶

Sur le graphique ci-dessous, chaque point représente un joueur de l'équipe de France de rugby ayant participé à la Coupe du monde 2015. La position du point correspond à la masse du joueur (en abscisses) et à sa taille (en ordonnée) ; la couleur du point correspond à son poste sur le terrain.

On se pose la question de savoir, pour un joueur de rugby dont on connaît la masse et la taille, quel serait le poste qu'il aurait le plus de chance d'occuper sur le terrain.

Question 10 : Si on suppose qu'un joueur J pèse 85 kg et mesure 1,78 m, déterminer le poste occupé par les cinq joueurs de l'équipe de France qui ont des mensurations les plus proches de J.

Question 11 : Si on suppose qu'un joueur J pèse 100 kg et mesure 1,90 m, déterminer le poste occupé par les sept joueurs de l'équipe de France qui ont des mensurations les plus proches de J.

L'algorithme des k plus proches voisins permet d'estimer le poste d'un joueur, à partir de sa masse et de sa taille, en regardant quel est le poste majoritaire parmi ses k voisins (c'est-à-dire les joueurs ayant les mensurations les plus proches des siennes). On parle aussi d'algorithme knn (k nearest neighbours).

Il s'agit d'un algorithme d'apprentissage puisqu'on estime une donnée inconnue par comparaison avec une série de données connues.

Le graphique ci-dessous est construit comme le précédent, mais en prenant en compte les joueurs de toutes les équipes nationales ayant participé à la Coupe du monde de 2015. Les données proviennent du fichier joueurs_rugby.csv.

Question 12 : Ecrire une fonction importer_donnees permettant de récupérer la taille, le poids et le poste de tous les joueurs ayant participé à la Coupe du monde 2015. Les données de chaque joueur seront stockées dans un dictionnaire ayant pour clés taille, poids et poste, et l'ensemble des dictionnaires sera stocké dans un tableau.

import csv

def importer_donnees():
    """
    Récupère la taille, le poids et le poste de tous les rugbymans ayant participé à la Coupe du monde 2015.
    - Sortie : tab (tableau dont les éléments sont des dictionnaires)
    """
    tab = []
    with open('joueurs_rugby.csv', 'r', encoding = 'utf-8') as fichier:
        donnees = csv.DictReader(fichier, delimiter = ',')
        for enregistrement in donnees:
            enreg = dict(enregistrement)
            dico = {'poste' : enreg['poste'],
                    'taille' : int(enreg['taille']),
                    'poids' : int(enreg['poids'])}
            tab.append(dico)
    return tab

Question 13 : Ecrire une fonction k_voisins qui prend en paramètres d'entrée un entier strictement positif k, un tableau de données donnees et deux nombres positifs taille et poids et qui renvoie un tableau contenant le poste des k joueurs de rugby ayant les mensurations les plus proches de taille et poids.

def k_voisins(k, donnees, taille, poids):
    """
    Détermine, parmi les donnees, quels sont les k joueurs qui ont les mensurations les plus proches
    de la taille et du poids passés en paramètres.
    - Entrées : k (entier, nombre de voisins souhaité), donnees (tableau de dictionnaires),
                taille, poids (nombres)
    - Sortie : tab (tableau de chaînes de caractères, les postes des k voisins les plus proches)
    """
    def cle_ecart(d):
        return d['ecart']
    
    for enreg in donnees:
        enreg['ecart'] = ((enreg['taille'] - taille) ** 2 + (enreg['poids'] - poids) ** 2) ** 0.5
    donnees.sort(key = cle_ecart)
    tab = [donnees[i]['poste'] for i in range(k)]
    return tab

Question 14 : Ecrire une fonction element_majoritaire qui prend en paramètre d'entrée un tableau et qui renvoie la valeur majoritaire dans le tableau. En cas d'ex aequo, la fonction renvoie une des valeurs majoritaires.

from random import choice

def element_majoritaire(tab):
    """
    Détermine l'élément majoritaire dans un tableau.
    - Entrée : tab (tableau)
    - Sortie : (élément majoritaire du tableau)
    """
    comptage = {}
    for elem in tab:
        if elem in comptage:
            comptage[elem] = comptage[elem] + 1
        else:
            comptage[elem] = 1
    poste_majoritaire, cpt = ['autre'], 0
    for poste in comptage:
        if comptage[poste] > cpt:
            poste_majoritaire = [poste]
            cpt = comptage[poste]
        elif comptage[poste] == cpt:
            poste_majoritaire.append(poste)
    return choice(poste_majoritaire)

Question 15 : Ecrire des lignes de code permettant de déterminer, grâce à l'algorithme des k plus proches voisins et pour différentes valeurs de k, le poste d'un joueur de rugby de 110 kg et 1,88 m.

joueurs = importer_donnees()
for k in range(3, 10):
    print(f"k = {k} --> {element_majoritaire(k_voisins(k, joueurs, 188, 110))}")

k = 3 --> 3e ligne
k = 4 --> 3e ligne
k = 5 --> 1e ligne
k = 6 --> 1e ligne
k = 7 --> 3e ligne
k = 8 --> 3e ligne
k = 9 --> 3e ligne

Ce que vous devez savoir¶

Ce que vous devez savoir :

Ecrire un algorithme de recherche séquentielle d'une valeur dans un tableau.
Savoir qu'un algorithme de recherche séquentielle a une complexité linéaire.
Ecrire un algorithme de recherche dichotomique d'une valeur dans un tableau trié.
Savoir qu'un algorithme de recherche dichotomique a une complexité logarithmique.
Déterminer le nombre d'itérations nécessaires pour trouver (par recherche dichotomique) une valeur donnée dans un tableau trié donné.
Connaître la notion de terminaison (et de variant de boucle) et la notion de correction partielle (et d'invariant de boucle) d'un algorithme.
Utiliser un algorithme glouton pour résoudre un problème d'optimisation.
Utiliser l'algorithme des k plus proches voisins.

Exercices bilan¶

Exercice 1¶

Exécuter l'algorithme de recherche dichotomique à la main pour le tableau suivant :

pour rechercher successivement dans le tableau :

la valeur 27.

La valeur 27 est trouvée en 2 itérations.

la valeur 6.

La valeur 6 est trouvée en 4 itérations.

la valeur 18.

La valeur 18 n'est pas trouvée, et sa recherche nécessite 5 itérations.

Exercice 2¶

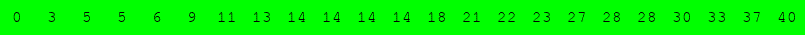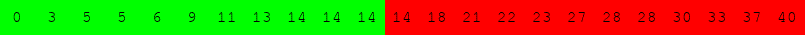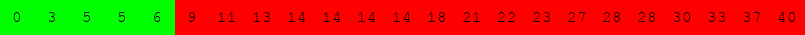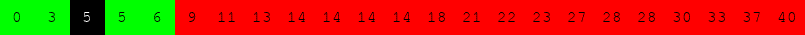
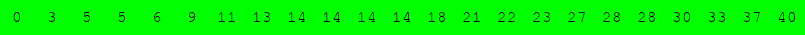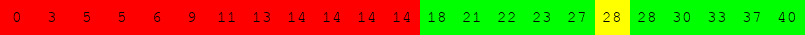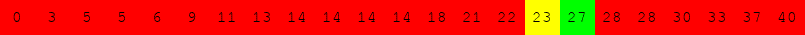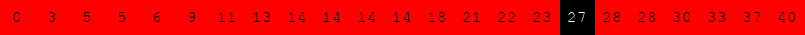
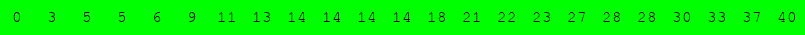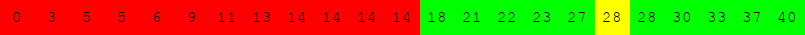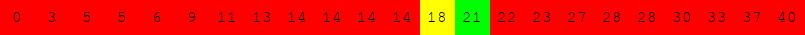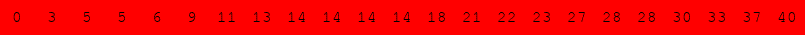
Voici une variante du problème du sac à dos.

Un libraire propose de racheter des livres à ses clients, et met en ligne une application qui permet aux clients d'estimer le prix de rachat de chaque livre par le libraire. Par contre, ce dernier refuse de reprendre plus d'un kilogramme de livres.

Voici la masse et la valeur estimée de six livres qu'un client est susceptible de revendre au libraire :

Livre	A	B	C	D	E	F
Valeur (en euros)	4,55	3,60	2,40	1,35	1,30	0,10
Masse (en grammes)	700	600	400	300	200	100

Lister toutes les combinaisons possibles qui peuvent être formées par le client et indiquer la somme d'argent que le client peut obtenir pour chaque combinaison.

Appliquer successivement les trois stratégies gloutonnes suivantes :

choisir les livres par ordre décroissant de valeur (parmi ceux dont la masse ne dépasse pas la capacité restante).

XXX

choisir les livres par ordre de masse décroissante.

XXX

choisir les livres par ordre décroissant de rapport valeur/masse (parmi ceux dont la masse ne dépasse pas la capacité restante).

XXX